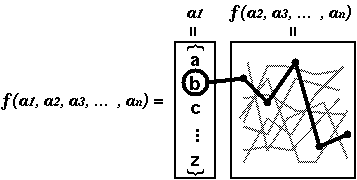
図 1. 再帰を使ったバージョン
概要: ある種の問題は、再帰を使うと非常に効率的に記述できる。 しかし大量のデータを生成するような再帰的手続きは厳密に制御する必要があり、 そういったプログラミングは難しい。Python 2.2 以降から使用可能になった ジェネレータを使うと、簡潔なコードを維持しつつ、 こうした手続きをかんたんに制御することができる。
この文書で使われているソースコードは こちら。 プレインテキスト版は こちら。
再帰は非常に強力なメカニズムです。 時にこれは混乱を招くこともありますが、ふつう再帰を使うと、問題を簡単に記述することができます。 ある手続きが扱うデータ量が指数的に増えるような場合、これはとくにあてはまります。 木構造の探索がいい例でしょう。木の各節点はひとつ以上の子を持っていますが、 下へ下へとたどっていくにつれて、節点の数は指数的に増えていきます。 でも、もしすべての節点が一様に同じ種類のものであれば、まったく同じ手続きが すべての節点に対してくりかえし適用できます。
でも木の探索はおそらくほどんどの計算機科学の教科書で 説明されているので、あまりおもしろくはありません。 誰でも木を探索するときには、ほとんど何も考えずに再帰を使うことでしょう。 しかし、もちろん再帰が役に立つような例はほかにも沢山あります。 そこでここでは別の例を見てみましょう。
以下のような関数 f を考えます。 これはベクトルの集合 (V1, V2, V3, ... , Vn) を引数としてとり、 Vi の各要素がとりうる組み合わせすべてからなる集合を 返すものとします。おのおのの組み合わせは、n要素のベクトル (xi1, xi2, ... , xim) からなります。ここで xij は Vi の要素です。この関数が返すベクトルはぜんぶで |V1| x |V2| x |V3| x ... x |Vn| 個あることになります。
この関数を Python で実装することを考えてみましょう。 単純さのため、ここではベクトル Vi のおのおのを 表すのに文字列オブジェクトを用いることにします。 この関数はベクトルの集合をリストとして返すことにしましょう。 すると、予想される結果は以下のようになります:
f([]) --> [''] # 1
f(['abc']) --> ['a', 'b', 'c'] # 3
f(['abc', 'xyz']) --> ['ax', 'ay', 'az', 'bx', 'by', 'bz', 'cx', 'cy', 'cz'] # 9
f(['abc', 'xyz', '123']) --> ['ax1', 'ax2', 'ax3', 'ay1', 'ay2', 'ay3', 'az1', 'az2', 'az3',
'bx1', 'bx2', 'bx3', 'by1', 'by2', 'by3', 'bz1', 'bz2', 'bz3',
'cx1', 'cx2', 'cx3', 'cy1', 'cy2', 'cy3', 'cz1', 'cz2', 'cz3'] # 27
一見すると、これは簡単に実装できそうに思えるかもしれません。 もしかすると再帰を使わなくても簡単に書けそうに見えるのではないでしょうか。 ではやってみましょう。
最初に、もし再帰をまったく使わないとすると、 プログラムはおそらくこんな感じのものになると思います:
def f0(args): counter = [ 0 for i in args ] r = [] while 1: r.append("".join([ arg1[i] for arg1,i in zip(args, counter) ])) carry = 1 x = range(len(args)) x.reverse() # x == [len(args)-1, len(args)-2, ..., 1, 0] for i in x: counter[i] += 1 if counter[i] < len(args[i]): carry = 0 break # "for" から抜ける counter[i] = 0 else: break # "while" から抜ける return r
再帰を使わない場合、プログラムはすべての組み合わせを生成するために
途中の状態を何らかの方法ですべて記憶しておかねばなりません。
このプログラムでは、全加算器 (full-adder) のようなものをエミュレートしました。
まずプログラムは整数のリストを準備します。そしてこの最下位の桁に 1 を加えようとします。
ループがまわるたびに、この関数は引数に渡された要素を結合して変数
r に入れていきます。しかしこのプログラムのふるまいは、
"carry" などの意味深長な変数名がヒントにはなるものの、
全体としてはわかりにくいものです。
では再帰を使うとどうなるでしょうか。関数 f は次のように再帰的に定義できます:
| f(Vi, Vi+1, ... , Vn) = | ({xi1} + f(Vi+1, ... , Vn)) + |
| ({xi2} + f(Vi+1, ... , Vn)) + | |
| ... | |
| ({xim} + f(Vi+1, ... , Vn)) . |
この定義を使って自分自身を呼び出すようにすると、プログラムはずっと簡単になります:
def fr(args): if not args: return [""] r = [] for i in args[0]: for tmp in fr(args[1:]): r.append(i + tmp) return r
これは非常に直接的に実装したものです。 再帰の便利なところは、ある問題をいくつかの「サブ問題」に 分割し、それらの各サブ問題にもまったく同じ手続きが使えることです。 このプログラムでは単に各引数の最初の要素をとってきて、 それをこの関数自身をひとつ少ない引数で呼びだしたときの すべての返り値に追加しています (図 1)。

これまで見てきた関数は、答えをいっぺんに返すようなものでした。 しかし探索や数え上げなどのアプリケーションによっては、 これらすべての組み合わせを覚えておく必要がない場合もあります。 やりたいのは、おのおのの組み合わせをただ検査して、 用が済んだらそれらは捨てるようにしたいのです。
出力の数が少ないときには、これは大した問題ではありません。 でも再帰的手続きで期待できるのは、その結果が指数的に増えるような場合でした。 ところが皮肉なことに、そのような関数はふつうかなり大量の出力を生成します。 これは問題です。多くの言語実装では、これらの出力すべてを記憶することは できません。おそかれはやかれ、記憶容量の限界に到達してしまうことでしょう:
$ ulimit -v 5000 $ python ... >>> for x in fr(["abcdefghij","abcdefghij","abcdefghij","abcdefghij","abcdefghij"]): ... print x ... Traceback (most recent call last): File "<stdin>", line 1, in ? File "<stdin>", line 7, in fr MemoryError
これに対する典型的な解法は、これらをすべて異なる状態に切りわけることです。 Python では、これはイテレータを使って行います。
Python では __iter__ メソッドをもつクラスは
イテレータとして使うことができます。イテレータは機能的にリストと
まったく同じではないものの、いくつかの関数あるいは文では
イテレータをリストのかわりに取ることができます (for, map,
filter など)。
class fi: def __init__(self, args): self.args = args self.counter = [ 0 for i in args ] self.carry = 0 return def __iter__(self): return self def next(self): if self.carry: raise StopIteration r = "".join([ arg1[i] for arg1,i in zip(self.args, self.counter) ]) self.carry = 1 x = range(len(self.args)) x.reverse() # x == [len(args)-1, len(args)-2, ..., 1, 0] for i in x: self.counter[i] += 1 if self.counter[i] < len(self.args[i]): self.carry = 0 break self.counter[i] = 0 return r # display def display(x): for i in x: print i, print return
このプログラムでは、クラス fi のコンストラクタは
再帰バージョンの関数 fr と同様に以下のようにして使うことができます:
>>> display(fi(["abc","def"]))
このインスタンスが for 文に渡されると、
__iter__ メソッドが呼ばれ、その返り値 (ここではそのインスタンス自身) が
ループのイテレータとして使われます。毎回ループをまわるたびにイテレータの
next メソッドが引数なしで呼ばれ、その返り値がループ変数に格納されます。
しかし、このプログラムを理解するのはそうやさしくはありません。
アルゴリズム的には、これは先にあげた再帰を使わないバージョンと
似ています。next が呼ばれるたびに、これは変数
counter に格納されている現在の状態を更新し、
その状態に応じた結果をひとつ返します。でもこれはさらに
こみ入っているように見えるでしょう。なぜならこのメソッドは
ループの中で呼ばれるようにできていますが、そのループ自体は
ここには明示的に現れないからです。読者はおそらくこのメソッドが
いきなり変数 carry をチェックしているのに
面くらうかもしれません。これを理解するには、このメソッドの
外側にあるループ (見えない) を想像する必要があるのです。
def fg(args): if not args: yield "" return for i in args[0]: for tmp in fg(args[1:]): yield i + tmp return
これはイテレータ版よりも簡単であるだけでなく、 再帰を使ったオリジナルのバージョンよりもさらに簡単になっていることに 気づきます。ジェネレータを使うと、結果を一回にひとつずつたんに投げていく (あるいは "yield していく") だけでよく、投げたあとは忘れることができます。 これは結果をストリームデバイスに表示するのに似ています。 状態を保存するよう気をつかう必要はありません。 ただすべての結果を何も考えずに生成し、それでいてなおかつ 手続きに対して厳密なコントロールを維持できるのです。 似た機能はいくつかの関数型言語でサポートされている「遅延評価 (lazy evaluation)」でも実現できることに気づかれるかもしれません。 遅延評価とジェネレータはまったく同じものではありませんが、 これらはどちらも同じ状況をべつべつのやり方で処理するのに役立ちます。
関数型プログラミングに慣れている人であれば、 オブジェクトよりも lambda 式によるカプセル化を好むかもしれません。 Python ではこれも可能です。しかし実際には、これはかなりむずかしいパズルでした。 イテレータと同じやり方でもできたのですが、ここではまったく別の方法を 試してみようと思ったのです。数時間にわたる試行錯誤のうえ、最終的に できたのは次のようなものでした:
def fl(args, i=0, tmp="", parent_sibling=None): if not args: # 葉にいる return (tmp, parent_sibling) if i < len(args[0]): # 隣の節点 (兄弟, sibling) を準備 sibling = fl(args, i+1, tmp, parent_sibling) return lambda: fl(args[1:], 0, tmp+args[0][i], sibling) else: # ひとつ上がって親の兄弟をたずねる return parent_sibling # lambda バージョンの探索ルーチン def traverse(n): while n: if callable(n): # 節点 n = n() else: # 葉 (result, n) = n print result, print
基本的なアイデアは、これを本当に木の探索として扱うというものです。
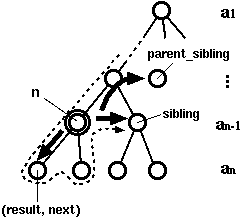
関数 f は各節点に部分的な解をもった木としてみることができます (図 2)。
fl が返す関数はその位置と隣の節点 (sibling)、および
親の節点の隣の節点を保持しています。この関数が木を下っていくにつれて
ベクトルの要素が追加されていきます。これが葉についたとき、
その関数はひとつの完全な解 (組み合わせ) を手にしているはずです。
同じ高さにもうそれ以上探索すべき節点がない場合、関数はひとつ上に上がって
親の隣へと進みます。この木を探索するには特別に用意された
関数 (ドライバ) が必要になります。
もちろん、ジェネレータ版でも木の探索をおこなうことはできます。 その場合、木の各節点で結果を投げていくということになるでしょう。